Nonparametric regression: Like parametric regression, but not
Initial thoughts
Nonparametric regression is similar to linear regression, Poisson regression, and logit or probit regression; it predicts a mean of an outcome for a set of covariates. If you work with the parametric models mentioned above or other models that predict means, you already understand nonparametric regression and can work with it.
The main difference between parametric and nonparametric models is the assumptions about the functional form of the mean conditional on the covariates. Parametric models assume the mean is a known function of \(\mathbf{x}\beta\). Nonparametric regression makes no assumptions about the functional form.
In practice, this means that nonparametric regression yields consistent estimates of the mean function that are robust to functional form misspecification. But we do not need to stop there. With npregress, introduced in Stata 15, we may obtain estimates of how the mean changes when we change discrete or continuous covariates, and we can use margins to answer other questions about the mean function.
Below I illustrate how to use npregress and how to interpret its results. As you will see, the results are interpreted in the same way you would interpret the results of a parametric model using margins.
Regression example
To illustrate, I will simulate data where the true model satisfies the linear regression assumptions. I will use a continuous covariate and a discrete covariate. The outcome changes for different values of the discrete covariate as follows:
\begin{equation*}
y = \left\{
\begin{array}{cccccccl}
10 & + & x^3 & & & + &\varepsilon & \text{if} \quad a=0 \\
10 & + & x^3 & – & 10x &+ & \varepsilon & \text{if} \quad a=1 \\
10 & + & x^3 & + & 3x &+ & \varepsilon & \text{if} \quad a=2 \\
\end{array}\right.
\end{equation*}
Here, \(x\) is the continuous covariate and \(a\) is the discrete covariate with values 0, 1, and 2. I generate data using the code below:
clear set seed 111 set obs 1000 generate x = rnormal(1,1) generate a = int(runiform()*3) generate e = rnormal() generate gx = 10 + x^3 if a==0 replace gx = 10 + x^3 - 10*x if a==1 replace gx = 10 + x^3 + 3*x if a==2 generate y = gx + e
Often the mean function is not known to the researchers. If I knew the true functional relationship between \(y\), \(a\), and \(x\), I could use regress to estimate the mean function. For now, I assume I do know the true relationship and estimate the mean function by typing
. regress y c.x#c.x#c.x c.x#i.a
Then I calculate the average of the mean function, the average marginal effect of \(x\), and average treatment effects of \(a\).
The average of the mean function is estimated to be \(12.02\), which I obtained by typing
. margins
Predictive margins Number of obs = 1,000
Model VCE : OLS
Expression : Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | 12.02269 .0313691 383.26 0.000 11.96114 12.08425
------------------------------------------------------------------------------
The average marginal effect of of \(x\) is estimated to be \(3.96\), which I obtained by typing
. margins, dydx(x)
Average marginal effects Number of obs = 1,000
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : x
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 3.957383 .0313871 126.08 0.000 3.89579 4.018975
------------------------------------------------------------------------------
The average treatment effect of \(a=1\), relative to \(a=0\), is estimated to be \(-9.78\). The average treatment effect of \(a=2\), relative to \(a=0\), is estimated to be \(3.02\). I obtained these by typing
. margins, dydx(a)
Average marginal effects Number of obs = 1,000
Model VCE : OLS
Expression : Linear prediction, predict()
dy/dx w.r.t. : 1.a 2.a
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
a |
1 | -9.776916 .0560362 -174.47 0.000 -9.886879 -9.666953
2 | 3.019998 .0519195 58.17 0.000 2.918114 3.121883
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
I now use npregress to estimate the mean function, making no assumptions about the functional form:
. npregress kernel y x i.a, vce(bootstrap, reps(100) seed(111))
(running npregress on estimation sample)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Bandwidth
------------------------------------
| Mean Effect
-------------+----------------------
Mean |
x | .3630656 .5455175
a | 3.05e-06 3.05e-06
------------------------------------
Local-linear regression Number of obs = 1,000
Continuous kernel : epanechnikov E(Kernel obs) = 363
Discrete kernel : liracine R-squared = 0.9888
Bandwidth : cross validation
------------------------------------------------------------------------------
| Observed Bootstrap Percentile
y | Estimate Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Mean |
y | 12.34335 .3195918 38.62 0.000 11.57571 12.98202
-------------+----------------------------------------------------------------
Effect |
x | 3.619627 .2937529 12.32 0.000 3.063269 4.143166
|
a |
(1 vs 0) | -9.881542 .3491042 -28.31 0.000 -10.5277 -9.110781
(2 vs 0) | 3.168084 .2129506 14.88 0.000 2.73885 3.570004
------------------------------------------------------------------------------
Note: Effect estimates are averages of derivatives for continuous covariates
and averages of contrasts for factor covariates.
The average of the mean estimate is \(12.34\), the average marginal effect of \(x\) is estimated to be \(3.62\), the average treatment effect of \(a=1\) is estimated to be \(-9.88\), and the average treatment effect of \(a=2\) is estimated to be \(3.17\). All values are reasonably close to the ones I obtained using regress when I assumed I knew the true mean function.
Furthermore, the confidence interval for each estimate includes both the true parameter value I simulated and the regress parameter estimate. This highlights another important point. In general, the confidence intervals I obtain from npregress are wider than those from regress with the correctly specified model. This is not surprising. Nonparametric regression is consistent, but it cannot be more efficient than fitting a correctly specified parametric model.
Using regress and margins and knowing the functional form of the mean is equivalent to using npregress in this example. You get similar point estimates and the results have the same interpretation.
Binary outcome example
Above I presented a result for a continuous outcome. However, the outcome does not need to be continuous. I can estimate a conditional mean, which is the same as the conditional probability, for binary outcomes.
The true model is given by
\begin{equation*}
y = \left\{
\begin{array}{cl}
1 & \text{if} \quad -1 + x – a + \varepsilon > 0\\
0 & \text{otherwise}
\end{array}\right.
\end{equation*}
where
\begin{equation*}
\varepsilon | x, a \sim \mathrm{Logistic} \left(0, \frac{\pi}{\sqrt{3}} \right)
\end{equation*}
And \(a\) again takes on discrete values 0, 1, and 2. The results of estimation using logit would be
. quietly logit y x i.a
. margins
Predictive margins Number of obs = 1,000
Model VCE : OIM
Expression : Pr(y), predict()
------------------------------------------------------------------------------
| Delta-method
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_cons | .486 .0137 35.47 0.000 .4591485 .5128515
------------------------------------------------------------------------------
. margins, dydx(*)
Average marginal effects Number of obs = 1,000
Model VCE : OIM
Expression : Pr(y), predict()
dy/dx w.r.t. : x 1.a 2.a
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .1984399 .0117816 16.84 0.000 .1753483 .2215315
|
a |
1 | -.1581501 .0347885 -4.55 0.000 -.2263344 -.0899658
2 | -.363564 .0319078 -11.39 0.000 -.426102 -.3010259
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.
The average of the conditional mean estimate is \(0.486\), which is the same as the average probability of a positive outcome; the marginal effect of \(x\) is estimated to be \(0.198\), the average treatment effects of \(a=1\) is estimated to be \(-0.158\), and the average treatment effects of \(a=2\) is estimated to be \(-0.364\).
Let’s see if npregress can obtain similar results without knowing the functional form is logistic.
. npregress kernel y x i.a, vce(bootstrap, reps(100) seed(111))
(running npregress on estimation sample)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Bandwidth
------------------------------------
| Mean Effect
-------------+----------------------
Mean |
x | .4321719 1.410937
a | .4 .4
------------------------------------
Local-linear regression Number of obs = 1,000
Continuous kernel : epanechnikov E(Kernel obs) = 432
Discrete kernel : liracine R-squared = 0.2545
Bandwidth : cross validation
------------------------------------------------------------------------------
| Observed Bootstrap Percentile
y | Estimate Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Mean |
y | .4840266 .0160701 30.12 0.000 .4507854 .5158817
-------------+----------------------------------------------------------------
Effect |
x | .2032644 .0143028 14.21 0.000 .1795428 .2350924
|
a |
(1 vs 0) | -.1745079 .0214352 -8.14 0.000 -.2120486 -.1249168
(2 vs 0) | -.3660315 .0331167 -11.05 0.000 -.4321482 -.300859
------------------------------------------------------------------------------
Note: Effect estimates are averages of derivatives for continuous covariates and
averages of contrasts for factor covariates.
The conditional mean estimate is \(0.484\), the marginal effect of \(x\) is estimated to be \(0.203\), the average treatment effects of \(a=1\) is estimated to be \(-0.174\), and the average treatment effects of \(a=2\) is estimated to be \(-0.366\). So, yes, it can.
Answering other questions
npregress provides marginal effects and average treatment effect estimates as part of its outcome, yet I can also obtain answers to other relevant questions using margins.
Let’s go back to the regression example.
Say I wanted to see the mean function at different values of the covariate \(x\), averaging over \(a\). I could type:
. margins, at(x=(1(.5)3)) vce(bootstrap, reps(100) seed(111))
(running margins on estimation sample)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Predictive margins Number of obs = 1,000
Replications = 100
Expression : mean function, predict()
1._at : x = 1
2._at : x = 1.5
3._at : x = 2
4._at : x = 2.5
5._at : x = 3
------------------------------------------------------------------------------
| Observed Bootstrap Percentile
| Margin Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_at |
1 | 9.309943 .1538459 60.51 0.000 9.044058 9.689572
2 | 10.96758 .2336364 46.94 0.000 10.53089 11.52332
3 | 14.78267 .311172 47.51 0.000 14.21305 15.50895
4 | 21.50949 .3955136 54.38 0.000 20.86696 22.34698
5 | 32.16382 .529935 60.69 0.000 31.10559 33.25611
------------------------------------------------------------------------------
and then, using marginsplot, I obtain the following graph:
Figure 1: Mean outcome at different values of x
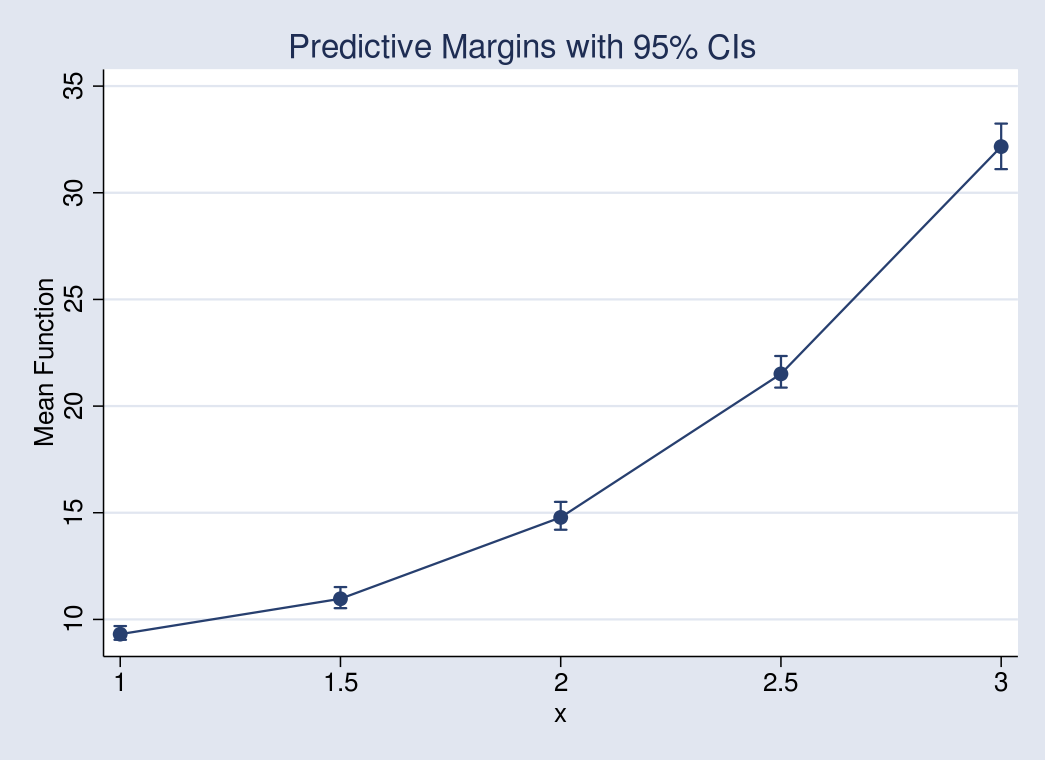
As \(x\) increases, so does the outcome. The increase is nonlinear. It is much greater for larger values of \(x\) than for smaller ones.
I could instead trace the mean function for different values of \(x\), but now, obtaining the expected mean for each level of \(a\) rather than averaging over \(a\), I type
. margins a, at(x=(-1(1)3)) vce(bootstrap, reps(100) seed(111))
and then use marginsplot to visualize the results:
Figure 2: Mean outcome at different values of x for fixed values of a
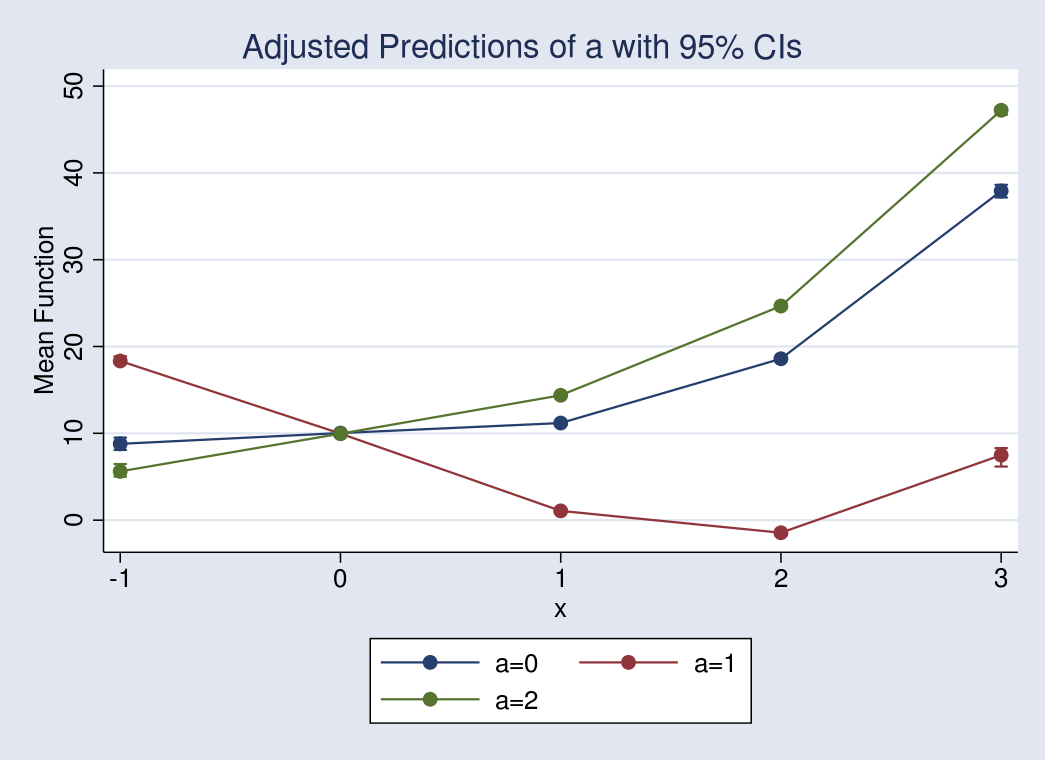
I see that the effect on the mean, as \(x\) increases, differs for different values of \(a\). Because our model has only two covariates, the graph above maps the whole mean function.
I could even ask what the average effect of a 10% increase in \(x\) is. By “average” in this case, I mean giving each observation in the dataset a 10% larger \(x\). Perhaps \(x\) is a rebate and I wonder what would happen if that rebate were increased by 10%. I type
. margins, at(x=generate(x*1.1)) at(x=generate(x))
> contrast(at(r) nowald) vce(bootstrap, reps(100) seed(111))
(running margins on estimation sample)
Bootstrap replications (100)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
Contrasts of predictive margins
Number of obs = 1,000
Replications = 100
Expression : mean function, predict()
1._at : x = x*1.1
2._at : x = x
--------------------------------------------------------------
| Observed Bootstrap Percentile
| Contrast Std. Err. [95% Conf. Interval]
-------------+------------------------------------------------
_at |
(2 vs 1) | -1.088438 .0944531 -1.31468 -.915592
--------------------------------------------------------------
I can use margins and npregress together to obtain effects at different points in my data, average effects over my population, or any question that would make sense with a parametric model in Stata.
Closing remarks
npregress estimates a mean function with all types of outcomes—continuous, binary, count outcomes, and more. The interpretation of the results is equivalent to the interpretation, and their usefulness is equivalent to that of margins after fitting a parametric model. What makes npregress special is that we do not need to assume a functional form. With parametric models, our inferences will likely be meaningless if we do not know the true functional form. With npregress, our inferences are valid regardless of the true functional form.